LIMIT FUNGSI

Limit Fungsi

Definisi

Berikut beberapa definisi limit fungsi yang umum diterima.

⛬ Limit merupakan sebuah konsep matematika dimana sesuatu dikatakan “hampir” atau “mendekati” nilai suatu bilangan tertentu. Limit dapat berupa sebuah fungsi yang kodomainnya “hampir” atau “mendekati” nilai suatu bilangan asli tertentu.

Fungsi pada garis bilangan riil

Bila f: R

\rightarrow

R terdefinisi pada garis bilangan riil, dan p, L

\in

R maka kita menyebut limit f ketika x mendekati p adalah L, yang ditulis sebagai:

\lim _{x\to p}f(x)=L

jika dan hanya jika untuk setiap ε > 0 terdapat δ > 0 sehingga |x - p|< δ mengimplikasikan bahwa |f (x) - L | < ε . Di sini, baik ε maupun δ merupakan bilangan riil. Perhatikan bahwa nilai limit tidak tergantung pada nilai f (p)

Limit searah

Limit saat: x → x₀⁺ ≠ x → x₀^-. Maka, limit x → x₀ tidak ada.

Masukan x dapat mendekati p dari atas (kanan di garis bilangan) atau dari bawah (kiri). Dalam hal ini limit masing-masingnya dapat ditulis sebagai

\lim _{x\to p^{+}}f(x)=L

atau

\lim _{x\to p^{-}}f(x)=L

Bila kedua limit ini sama nilainya dengan L, maka L dapat diacu sebagai limit f(x) pada p . Sebaliknya, bila keduanya tidak bernilai sama dengan L, maka limit f(x) pada p tidak ada.

Definisi formal adalah sebagai berikut.

Limit f(x) saat x mendekati p dari atas adalah L bila, untuk setiap ε > 0, terdapat sebuah bilangan δ > 0 sedemikian rupa sehingga |f(x) - L| < ε pada saat 0 < x - p < δ. Limit f(x) saat x mendekati p dari bawah adalah L bila, untuk setiap ε > 0, terdapat bilangan δ > 0 sehingga |f(x) - L| < ε bilamana 0 < p - x < δ.

Bila limitnya tidak ada terdapat osilasi matematis tidak nol.

Limit fungsi pada ketakhinggaan

Limit fungsi ini ada pada ketakhinggaan.

Bila dua unsur, ketakhinggaan positif dan negatif {-∞, +∞}, ditambahkan pada garis bilangan riil, kita dapat mendefinisikan limit fungsi pada ketakhinggaan. Dua unsur tambahan ini bukanlah bilangan, namun berguna dalam memerikan kelakuan limit pada kalkulus dan analisis.

Bila f(x) adalah fungsi riil, maka limit f saat x mendekati tak hingga adalah L, dilambangkan sebagai:

\lim _{x\to \infty }f(x)=L,

jika dan hanya jika untuk semua ε > 0 terdapat S > 0 sedemikian rupa sehingga |f (x) - L| < ε bilamana x > S.

Dengan cara yang sama, limit f saat x mendekati tak hingga adalah tak hingga, dilambangkan oleh

\lim _{x\to \infty }f(x)=\infty ,

jika dan hanya jika bila untuk semua R > 0 terdapat S > sedemikian sehingga f(x) > R bilamana x > S.

Limit Fungsi Aljabar dituliskan dengan:

Maksudnya, apabila x mendekati a namun x tidak sama dengan a maka f(x) mendekati L. Pendekatan x ke a dapat dilihat dari dua sisi yaitu sisi kiri dan sisi kanan atau dengan kata lain x dapat mendekati dari arah kiri dan arah kanan sehingga menghasilkan limit kiri dan limit kanan.

Dalam pengoperasian limit fungsi aljabar, terdapat beberapa hukum atau teorema limit yang perlu diperhatikan. Jika k konstanta, fungsi f dan fungsi g adalah fungsi-fungsi memiliki nilai limit yang mendekati bilangan c, maka:

No	TEOREMA
1	$\lim \limits_{x\to c}k=k$
2	$\lim \limits_{x\to c}x = c$
3	$k \cdot \lim \limits_{x\to c}f(x)$
4	$\lim \limits_{x \to c}({f(x) + g(x)})$ $= \lim_{x\to c}f(x) + \lim_{x\to c}g(x)$
5	$\lim \limits_x\to c({f(x) - g(x)}) = \lim_x\to c{f(x) - g(x)}$ $= \lim_x{\to c}f(x) - \lim_{x \to c}g(x)$
6	$\lim \limits_{x\to c}({f(x) \cdot g(x)}) = \lim_{x\to c}f(x) \cdot \lim_{x\to c}g(x)$
7	$\lim \limits_{x\to c}\frac{f(x)}{g(x)} = \frac{\lim_{x\to c}f(x)}{\lim_{x\to c}g(x)}$
8	$\lim \limits_{x\to c}(f(x)^n) = (\lim_{x\to c}f(x))^n$
9	$\lim \limits_{x\to c}(\sqrt[n]{f(x)}) = \sqrt[n]{\lim_{x\to c}f(x)}$

Menentukan Nilai Limit Fungsi Aljabar

🔥Ada 2 bentuk dalam menentukan limit fungsi aljabar yaitu:

Bentuk pertama

$\lim_{x\rightarrow a}f(x)$

Bentuk kedua

$\lim_{x\rightarrow \sim }f(x)$

🔥Ada tiga metode dalam mengerjakan limit fungsi aljabar, yaitu:

1. Metode substitusi

Metode paling mudah dengan menentukan hasil suatu limit fungsi adalah dengan mensubstitusi langsung nilai kedalam fungsi f(x). Syarat metode ini adalah jika hasil substitusi tidak membentuk nilai “tak tentu”. Contoh:

$\lim \limits_{x\to 3}\frac{x^2 - 4}{x + 2} = \frac{9 - 4}{3 + 2} = 1$

👇contoh lain:

1. Tentukan nilai limit fungsi aljabar dari
$\lim_{x\rightarrow 1}\ 3x-1=3(1)-1=3-1=2$

Jadi, nilai dari limit fungsi aljabar tersebut, $\lim_{x\rightarrow 1}\ 3x-1=2$

2. Tentukan nilai limit fungsi aljabar dari
$\lim_{x\rightarrow 2}\ 2x^{2}+5=\ 2(2)^{2}+5=\ 2(4)+5=\ 8+5=\13$

Jadi, nilai dari limit fungsi aljabar tersebut,
$\lim_{x\rightarrow 2}\ 2x^{2}+5=\ 13$

2. Metode pemfaktoran

Jika pada metode substitusi menghasilkan suatu nilai bentuk tak tentu seperti:

∞, $\frac{0}{0}$ , $\frac{\infty}{\infty}$ , 0 x∞, ∞ – ∞, 00, ∞0, atau ∞∞

maka fungsi tersebut harus difaktorkan terlebih dahulu sehingga bentuknya tidak menjadi bentuk tak tentu, baru kemudian bisa disubstitusikan $x\to c$ . Contoh:

$\lim \limits_{x\to 3}\frac{x^2 - 3x}{2x - 6} = \frac{x(x - 3)}{2(x - 3)} = \frac{3}{2}$

Cara pemfaktoran digunakan apabila cara substitusi menghasilkan nilai limit yang tidak terdefinisikan seperti pada contoh berikut:
$\lim_{x\rightarrow 2}\ \frac{x^{2}-4}{x-2}=\ \frac{(2)^{2}-4}{2-2}=\ \frac{4-4}{2-2}=\ \frac{0}{0}$

👇contoh lain:

$\lim_{x\rightarrow 2}\ \frac{x^{2}-4}{x-2}=\lim_{x\rightarrow 2} \frac{{{\color{Red} (x-2)}}{(x+2)}}{{\color{Red} (x-2)}}=\lim_{x\rightarrow 2}\ (x+2)=\ (2)+2=\ 4$

Jadi, nilai dari limit fungsi aljabar tersebut,
$\lim_{x\rightarrow 2}\ \frac{x^{2}-4}{x-2}=\ 4$

Tentukan nilai limit fungsi aljabar dari
$\lim_{x\rightarrow 2}\ \frac{x-2}{\sqrt{x}-\sqrt{2}}=\ \lim_{x\rightarrow 2}\frac{{\color{Red} (\sqrt{x}-\sqrt{2})}(\sqrt{x}+\sqrt{2})}{{\color{Red} (\sqrt{x}-\sqrt{2})}}$
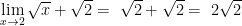
$\lim_{x\rightarrow 2}\sqrt{x}+\sqrt{2}=\ \sqrt{2}+\sqrt{2}=\ 2\sqrt{2}$

Jadi, nilai dari limit fungsi aljabar tersebut,
$\lim_{x\rightarrow 2}\sqrt{x}+\sqrt{2}=\ 2\sqrt{2}$

3. Metode perkalian dengan akar sekawan

Metode ini digunakan jika pada metode substitusi langsung menghasilkan nilai limit yang irasional. Fungsi dikalikan dengan akar sekawannya agar bentuk limit tersebut tidak irasional, sehingga bisa dilakukan kembali substitusi langsung nilai $x\to c$ . Contoh:

$\lim \limits_{x\to -1}\frac{x +1}{1 - \sqrt{x + 2}} x (\frac{1 + \sqrt{x +2}}{1 + \sqrt{x + 2}}) = \frac{(x + 1)(1 + \sqrt{x+ 2})}{1 - (x + 2)}$

$=\frac{(x + 1)(1+\sqrt{x+2})}{-x - 1} = \frac{(x+1)(1+\sqrt{x+2})}{-(x+1)} = -(1 + \sqrt{x + 2})$

$=-(1 + \sqrt{-(1) + 2}) = -(1 + 1) = -2$

Dalam pengoprasian limit fungsi aljabar, terkadang nilai x mendekati tak berhingga (∞), sehingga jika disubstitusikan fungsi menghasilkan nilai tak tentu. Dalam pengoperasian limitnya, terdapat beberapa hukum atau teorema limit yang perlu diperhatikan. Jika n adalah bilangan bulat, k konstanta, fungsi f dan fungsi g adalah fungsi-fungsi memiliki nilai limit yang mendekati bilangan c, maka:

No	TEOREMA	SYARAT
1	$\lim \limits_{x\to \infty}k = k$	k adalah konstanta
2	$\lim \limits_{x\to \infty}x^n = \infty$
2	$\lim \limits_{x\to \infty}\frac{1}{x^n} = 0$
3	$\lim \limits_{x\to -\infty}\frac{1}{x^n} = \infty$	Jika n = genap
3	$\lim \limits_{x\to - \infty}\frac{1}{x^n}= - \infty$	Jika n = ganjil
4	$\lim \limits_{x\to \infty}k \cdot f(x) = k \cdot \lim \limits_{x\to \infty}f(x)$	k adalah konstanta
5	$\lim \limits_{x\to \infty}({f(x) + g(x)}) = \lim \limits_{x\to \infty} f(x) + \lim \limits_{x\to \infty}g(x)$ $\lim \limits_{x\to \infty}{f(x) + g(x)} = \lim \limits_{x\to \infty} f(x) + \lim \limits_{x\to \infty}g(x)$
6	$\lim \limits_{x\to \infty}({f(x) - g(x)})$ $= \lim \limits_{x\to \infty}f(x) - \lim \limits_{x\to \infty}g(x)$
7	$\lim \limits_{x\to \infty}({f(x) \cdot g(x)}) = \lim \limits_{x\to \infty}f(x) \cdot \lim \limits_{x\to \infty} g(x)$
8	$\lim \limits_{x\to \infty}\frac{f(x)}{g(x)} = \frac{\lim \limits_{x\to \infty}f(x)}{\lim \limits_{x\to \infty}g(x)}$
9	$\lim \limits_{x\to c}(f(x)^n) = (\lim \limits_{x\to c} f(x))^n$
10	$\lim \limits_{x\to c}(\sqrt[n]{f(x)}) = \sqrt[n]{\lim \limits_{x\to c}f(x)}$
11	$\lim \limits_{x\to \infty}\frac{1}{f(x)} = \infty$	$\lim \limits_{x\to \infty}f(x) = 0$
11	$\lim \limits_{x\to \infty}\frac{1}{f(x)} = 0$	$\lim \limits_{x\to \infty}f(x) = \infty$

🔥Ada dua metode dalam mengerjakan limit fungsi aljabar bentuk tak berhingga:

Membagi dengan pangkat tertinggi

Metode ini digunakan pada limit fungsi bentuk $\lim \limits_{x\to \infty}\frac{f(x)}{g(x)}$ . Metode ini dapat dikerjakan dengan membagi pembilang f(x) dan penyebut g(x) dengan variabel xn berpangkat tertinggi yang ada dalam fungsi f(x) dan g(x). Setelahnya, baru dapat disubstitusi dengan $x\to \infty$ . Contoh:

$\lim \limits_{x\to \infty}\frac{4x-1}{x^2+2} = \frac{\frac{4x}{x^2} - \frac{1}{x^2}}{\frac{x^2}{x^2} + \frac{2}{x^2}} = \frac{\frac{4}{x} - \frac{1}{x^2}}{1+\frac{2}{x^2}} = \frac{0}{1} = 0$

Mengalikan bentuk sekawan

Metode ini digunakan pada limit fungsi bentuk $\lim \limits_{x\to \infty}f(x) - \lim \limits_{x\to \infty}g(x)$ . Metode ini dapat diselesaikan dengan perkalian bentuk sekawan:

$\frac{\lim \limits_{x\to \infty}f(x)+\lim \limits_{x\to \infty}g(x)}{\lim \limits_{x\to \infty}f(x)+\lim \limits_{x \to \infty}g(x)}$

kemudian dilanjutkan pembagian dengan metode pertama yaitu membagi dengan pangkat tertinggi. Contoh:

$\lim \limits_{x\to \infty}(\sqrt{x^2 + 4x - 5 - \sqrt{x^2 -x -2}})$

$=\lim \limits_{n\to \infty}(\sqrt{x^2 + 4x -5 - \sqrt{x^2 - x - 2}})$ $x \frac{(\sqrt{x^2+4x-5 + \sqrt{x^2 - x - 2}})}{(\sqrt{x^2+4x-5} + \sqrt{x^2-x-2})}$

$= \lim \limits_{n\to \infty}\frac{((x^2+4x-5) - (x^2-x-2))}{(\sqrt{x^2+4x-5} + \sqrt{x^2-x-2})}$ $= \lim \limits_{n\to \infty}frac{5x-3}{(\sqrt{x^2+4x-5})+\sqrt{x^2-x-2}}$

Kemudian pembilang dan penyebut dibagi x pangkat tertinggi yaitu x1:

$\lim \limits_{n\to \infty}\frac{\frac{5x}{x}-\frac{3}{x}}{(\sqrt{\frac{x^2+4x-5}{x^2}}+\sqrt{\frac{x^2-x-2}{x^2}})}$ $= \lim \limits_{n\to \infty}\frac{5-\frac{3}{x}}{(\sqrt{1+\frac{4}{x}-\frac{5}{x^2}}+ \sqrt{1-\frac{1}{x}-\frac{2}{x^2}})}$

$= \frac{(-0}{(1+1)} = \frac{5}{2}$

Limit Fungsi Trigonometri

Limit juga dapat digunakan pada fungsi trigonometri. Penyelesaiannya sama dengan fungsi limit aljabar. Namun, agar mengerti penjalasan selanjutnya harus mengerti terlebih dahulu konsep dari trigonometri. Penyelesaian dalam limit fungsi ini dalam trigonometri bisa dilakukan dengan melakukan perubahan-perubahan bentuk sinus, cosinus, dan tangen.

Ada tiga bentuk umum dalam limit fungsi trigonometri, yaitu bentuk :

1. Bentuk $\lim_{x\to c}f(x) = f(c)$

Pada bentuk ini, limit dari fungsi trigonometri f(x) merupakan hasil dari substitusi nilai c ke dalam x dari trigonometri. Contoh :

No.	CONTOH	NILAI LIMIT
1	$\lim \limits_{x\to ^\pi/_4} \sin 2x$	$\sin \frac{\pi}{2}$
2	$\lim \limits_{x\to \pi} \cos \frac{1}{2}x$	$cos\frac{1}{2}\pi$
3	$\lim \limits_{x\to ^\pi/_2} \tan x$	$\tan\frac{\pi}{2}$

Jika c = 0, maka rumus limit-limit trigonometrinya adalah sebagai berikut :

$\lim \limits_{x\to 0} \sin x = 0$
$\lim \limits_{x\to 0} \cos x = 1$
$\lim \limits_{x\to 0} \cos x = 0$

2. Bentuk $\lim_{x\to c}\frac{f(x)}{g(x)}$

Pada bentuk ini, limit diperoleh dari perbandingan 2 trigonometri berbeda. Kedua trigonometri tersebut jika langsung disubstitusi dengan nilai c menghasilkan f(c) = 0 dan g(c) = 0. Sehingga, nilai limit trigonometri tersebut menjadi bilangan tak tentu $\frac{0}{0}$ . Penyelesaiannya sama dengan limit fungsi aljabar yaitu pemfaktoran. Contoh bentuk ini yaitu:

$\lim \limits_{x\to ^\pi/_2}\frac{\sin 2x}{cosx} = \frac{2 \cos x \sin x}{cosx} = 2 \sin x = 2 \sin \frac{\pi}{2} = 2$

3. Bentuk $\lim_{x\to 0}\frac{f(x)}{g(x)}$

Pada bentuk ini, limit diperoleh dari perbandingan antara trigonometri dan fungsi aljabar. Jika disubstitusikan langsung akan menghaslikan bilangan tak tentu. Pada bentuk ini dikerjakan dengan konsep turunan. Bentuk rumus dasar limit ini adalah:

$\lim \limits_{x\to 0}\frac{\sin x}{x} = \lim_{x\to 0}\frac{x}{\sin x} = 1$
$\lim \limits_{x\to 0}\frac{x}{\cos x} = 0$
$\lim \limits_{x\to 0}\frac{\cos x}{x} = \infty$
$\lim \limits_{x\to 0}\frac{\tan x}{x} = \lim_{x\to}\frac{x}{\tan x} = 1$

Berdasarkan rumus dasar diataas, jika dikembangkan menjadi rumus-rumus berikut:

$\lim \limits_{x\to 0}\frac{\sin ax}{bx} = \frac{a}{b}$
$\lim \limits_{x\to 0}\frac{ax}{\sin bx} = \frac{a}{b}$
$\lim \limits_{x\to 0}\frac{ax}{\cos bx} = 0$
$\lim \limits_{x\to 0}\frac{\cos ax}{bx} = \infty$
$\lim \limits_{x\to 0}\frac{\tan ax}{bx} = \frac{a}{b}$
$\lim \limits_{x\to 0}\frac{ax}{\tan bx} = \frac{a}{b}$
$\lim \limits_{x\to 0}\frac{\sin ax}{\tan bx} = \frac{a}{b}$
$\lim \limits_{x\to 0}\frac{\tan ax}{\sin bx} = \frac{a}{b}$

👇Contoh Soal Limit Fungsi dan Pembahasan

Contoh Soal Limit 1

Tentukanlah nilai dari $\lim_{x\to 2}(\frac{6-x}{x^2-4} - \frac{1}{x-2})$ (UAN 2002)

Pembahasan 1 :

$\lim \limits_{x\to 2}(\frac{6-x}{x^2} - \frac{1}{x-2}) = \lim \limits_{x\to 2}(\frac{6-x}{x^2-4} - \frac{x+2}{(x-2)(x+2)})$ $= \lim \limits_{x\to 2}\frac{(6-x) - (x+2)}{(x-2)(x+2)}$

$=\lim \limits_{x\to 2}\frac{4-2x}{(x-2)(x+2)} = \lim \limits_{x\to 2}\frac{-2(x-2)}{(x-2)(x+2)}$ $= \lim \limits_{x\to 2}\frac{-2}{(x+2)}$

$=-\frac{2}{4} = -\frac{1}{2}$

Contoh Soal Limit 2

Tentukanlah nilai dari $\lim \limits_{x\to \infty}(\frac{\sqrt{4x+x^2} - \sqrt{2+x^2}}{3x})$ (UN 2009)

Pembahasan 2:

$\lim \limits_{x\to \infty}(\frac{\sqrt{4x+x^2}-\sqrt{2+x^2}}{3x}) = \lim_{x\to \infty}(\frac{\sqrt{\frac{4}{x^2}+\frac{x^2}{x^2}}-\sqrt{\frac{2}{x^2}+\frac{x^2}{x^2}}}{\frac{3x}{x}})$ $= \lim_{x\to \infty}(\frac{\sqrt{\frac{4}{x^2}+1}-\sqrt{\frac{2}{x^2}+1}}{3})$

$=(\frac{1-1}{3}) = \frac{0}{3} = 0$

Contoh Soal Limit 3

Tentukanlah nilai dari $\lim \limits_{x\to 0}(\frac{x^2+ \sin x \tan x}{1- \cos 2x})$ (SPMB 2002)

Pembahasan 3 :

$\lim \limits_{x\to 0}(\frac{x^2+ \sin x \tan x}{1- \cos 2x}) = \lim \limits_{x\to 0}(\frac{x^2+ \sin x \tan x}{2sin^2x})$ $= \lim \limits_{x\to 0}(\frac{x^2}{2 \sin^2x}+\frac{\sin x \tan x}{2sin^2x})$

$= \lim \limits_{x\to 0}(\frac{x^2}{2sin^2x}+\frac{\sin x \tan x}{2 \sin^2x})$ $= \lim \limits_{x\to 0}(\frac{x^2}{2 \sin^2x}+\frac{\tan x}{2 \sin x})$

$=(\frac{1}{2(1^2)}+\frac{1}{2(1)}) = \frac{1}{2}+\frac{1}{2} = 1$

Cari Blog Ini

yulias blog